Modular Networks: Learning to decompose neural computation
UPDATE 17. December 2018
For a more detailed description of the idea space around conditional computation and sparsity see my new technical report (Kirsch October 2018).
Recently, I thought a lot about the concept of modularity in artificial neural networks and wrote a paper on the topic. In this blog post, I will discuss my findings and possible future work in detail.
Currently, our largest neural networks have only billions of parameters, while the brain has trillions of synapses that are arguably even more complex than simple multiplication. To this date, we are not able to scale up artificial neural networks to trillions of parameters by performing the usual dense matrix multiplication. It is questionable whether this dense matrix multiplication approach would make sense anyways, given that the brain certainly has sparse connectivity and sparse activations. Likewise, in a previous experiment, I was able to show that activations in artificial neural networks are already sparse or can be even more sparse by introducing L1 regularization. The following figure visualizes this phenomenon for the task of image classification on the CIFAR10 dataset.
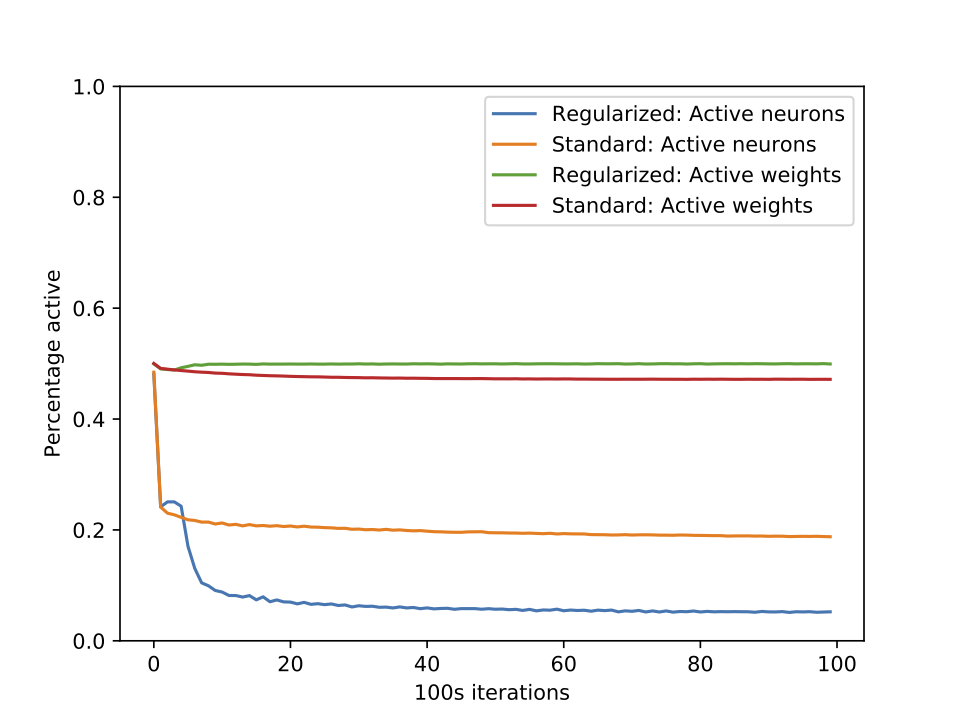
The regularized version had a L1 regularizer applied to both weights and activations (with similar test accuracy).
While the brain saves energy when not activating neurons, due to our dense matrix multiplication we do not have similar gains. Furthermore, there is evidence that the brain develops a modular structure in order to optimize energy cost, improve adaptation to changing environments and mitigate catastrophic forgetting. Sounds like we should try and implement some modularity for our artificial neural networks too!
Modular Networks
Inspired by these findings, I developed a generalized Expectation Maximization algorithm that allows decomposing neural computation into multiple modules. At the core of it, we have the modular layer, as seen in the following figure.
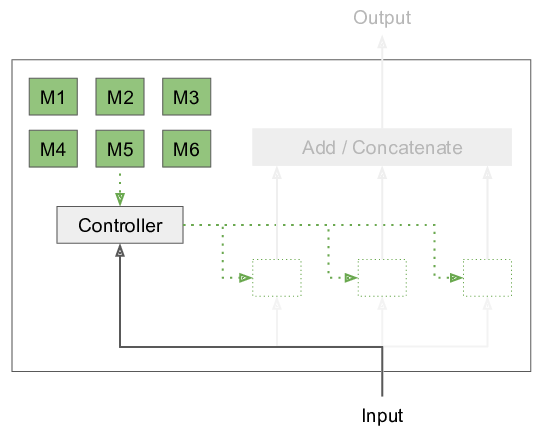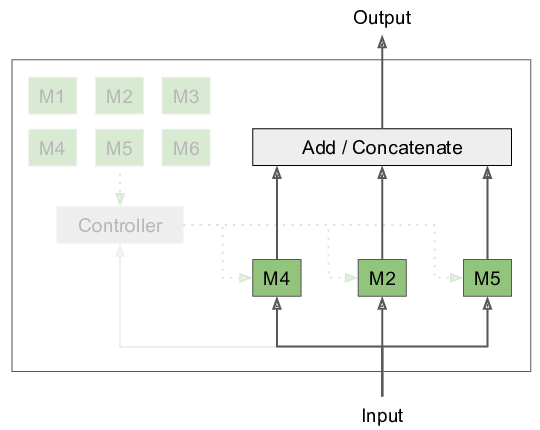
The controller picks from the modules M1 to M6 (which are arbitrary differentiable functions) based on the given input and executes them. Therefore, depending on the input, we evaluate different parts of the network – in effect modularizing our neural network architecture. Now we can just stack this modular layer or insert it arbitrarily into existing architectures, for instance, a recurrent neural network. Both the decomposition of functionality into modules, as well as the parameters of the modules, are learned. More details can be found in my publication.
Learnings from my research
Ultimately my goal was to make modular learning a tool for large, scalable architectures that are less prone to catastrophic forgetting and would, therefore, be suitable for life-long learning. The idea was that if gradients need only be propagated through very few modules of a large pool of potentially thousands of modules, then it might be easier to prevent it from damaging other functionality for different tasks or datapoints. Given that we’d like to optimize only the parameters of a small set of modules, one easy method might be to add other data samples to the mini-batch that are also assigned to these selected modules.
But it turns out, learning this kind of modularity has problems in itself – both conceptually, as well as technically.
Generalization vs Specialization. Naturally, each module is supposed to specialize in certain aspects of the training data. For instance, in my research, I showed how a word-level language model had modules that focused on different semantics such as the beginning of a sentence or quantitative words. But of course, in machine learning, we also aim to generalize to unseen datapoints. This kind of modularization leads to specialization that might hurt generalization by specializing on aspects of the data that may only exist in the training set. Indeed, we showed that modularization does not generalize very well for image classification on the CIFAR10 dataset. Interestingly, this issue was less severe for language modeling and therefore depends on the modality of the data. One open question remains: How do we make sure that specialization occurs only such that computational efficiencies are gained but generalization remains uninhibited?
Not every problem might be a composition of modules. By learning the composition of modules we are somewhat enforcing that the problem is decomposable – how do we know this is even true? While it might make sense to split language understanding and visual understanding into two different brain regions, does it necessarily make sense to also subdivide vision further into discrete module choices?
Reduced learning signal for each module for smaller datasets. Because modules are only active for some datapoints, the number of samples that each of these modules is trained on is significantly reduced. This means we either require even larger datasets or this may further reduce the generalization ability of each module. It might be worth investigating whether larger datasets can reduce the effect of overfitting, such as unsupervised image reconstruction for the domain of images.
Inefficiencies because of lack of batching. This is not an inherent problem of modularity but a technical one. We are splitting a mini batch of data and distribute the datapoints to different modules ultimately resulting in smaller batch sizes for each of the modules. Because our GPU architectures are efficient in parallelizing matrix multiplication smaller batch sizes mean slower computation. There are workarounds to increase the batch-size dramatically and distribute computation to multiple workers in a distributed environment, but this requires significant engineering effort. This paper demonstrates how this can be done.
Alternatives for modular learning and conditional computation
Putting modularity aside, there might be another way to achieve computational benefits through the observed sparsity by leveraging sparse matrix-matrix multiplication. As we’ve seen previously, about 90% of all activations can be zero – effectively making 90% of the weight matrix irrelevant. This might be a very interesting direction for future research. Of course, this will still distribute computation over the entire network instead of localizing it into modules. Therefore, it is unclear whether we can yield any mitigation of catastrophic forgetting in this way.
Another interesting aspect I would like to investigate is whether modularity naturally occurs in artificial neural networks. Could we create a graph of co-activity of neurons to see whether functionality clusters into modules automatically? If this modularization does not occur, might it be beneficial to introduce a soft locality constraint that moves correlated activations together such that larger parts of the matrix need not be computed entirely because these correspond to ‘inactive modules’?